But what about middle school and high school teachers? And what about teachers of students with learning disabilities—at any grade level?
To many, the use of visuals is an elementary school practice. Counting on fingers, modeling with stick figures, and coloring in bar graph worksheets seem like appropriate strategies for young students who are learning foundational math concepts. In older grade levels, visual representations are often highlighted in the first or second instructional example per the guidance of the textbook, but they are rarely emphasized as a critical part of the lesson.
However, they should be emphasized more often!

The Importance of Visual Representations
Research suggests that visual representations are critical to the success of math students at all ages and ability levels, especially those with learning disabilities. There’s an important caveat to these research findings, though. Simply adding a picture or a diagram to a word problem for additional context is far less helpful than explicitly teaching students how to use a particular visual representation to solve the problem. Explicit instruction with visual representations includes plenty of opportunities for students to practice, get feedback, and ask questions. These include pictures and drawings, diagrams, graphs, physical gesturing, and manipulatives. As students become more adept at using visuals, the cognitive demand for solving the problem lessens. In other words, it gets easier for them to solve math problems.
Students respond better to visuals that the teacher prescribes than to those they select on their own. This may be surprising to some, especially as much of the current conversation in education involves student-centered learning. Yes, it is important to empower students to make meaning of their own learning. But the role of the teacher cannot be understated. Students depend on their teacher to guide them through their problem-solving processes by offering models, correction, suggestion, and encouragement along the way. For example, students typically do not intuitively know how to use fraction tiles to compare fractions with unlike denominators. They need their teacher to set up structured opportunities for them to explore fraction comparison with these manipulatives.
Unique Learning System is an excellent example of a curriculum that emphasizes the importance and relevance of visuals throughout its math lessons. It is designed to meet the needs of learners with diverse communication and cognitive needs and pairs math vocabulary, math symbols, and pictorial representations in every lesson. Teachers can supplement the visual representations as needed to scaffold up or down.
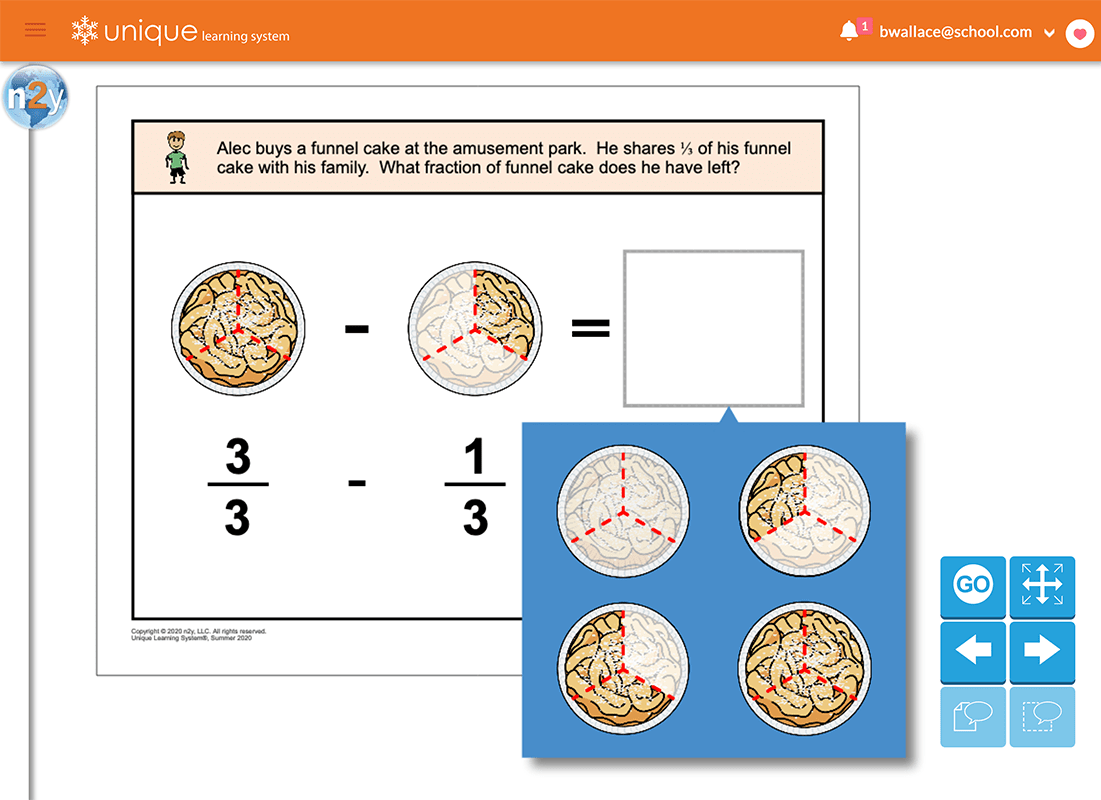
Example
Using Visuals to Teach Perimeter
A middle school math special education teacher is planning her upcoming geometry unit, and she knows from experience that many students confuse perimeter and area, especially when the two problem types are mixed throughout a worksheet (e.g., a problem on finding the perimeter of a rectangle followed by a problem on finding the area of a square). In the past, she typically has started this unit by teaching perimeter. She shows students how to calculate perimeter by drawing a 2D shape on the board and labeling the sides of the shape with their measurements. She then models how to add those measurements to calculate the total distance around the shape. Students write “total distance around a shape = perimeter” in their notebooks.
To incorporate more visuals into her teaching, she might try these strategies:
- Begin with a kinesthetic activity that introduces students to the concept of distance in a tangible way. Offer standard and nonstandard tools to measure the distance around the classroom. Use anything from yardsticks or measuring tapes to shoes or chairs. Students will be immediately engaged as they are able to move about, work together, and use tools that are familiar.
- Provide explicit instruction on calculating perimeter by following the steps described above. After this, teach students to identify the problem as a “perimeter problem” and label the problem with a capital letter, P. This will become important when students are asked to distinguish between perimeter problems and area problems later in the unit.
- Next, model for students how to use a highlighter to trace the perimeter of the 2-D shape. This simple but powerful visual representation of “distance around” reinforces the concept of perimeter and reminds students that they must account for and label all sides of the shape.
Using Pictures to Support Context
Teachers know that pictures are a helpful accommodation for English language learners (ELLs) and struggling readers. These kinds of pictures serve a different purpose than those that visually represent the mathematics of the problem.
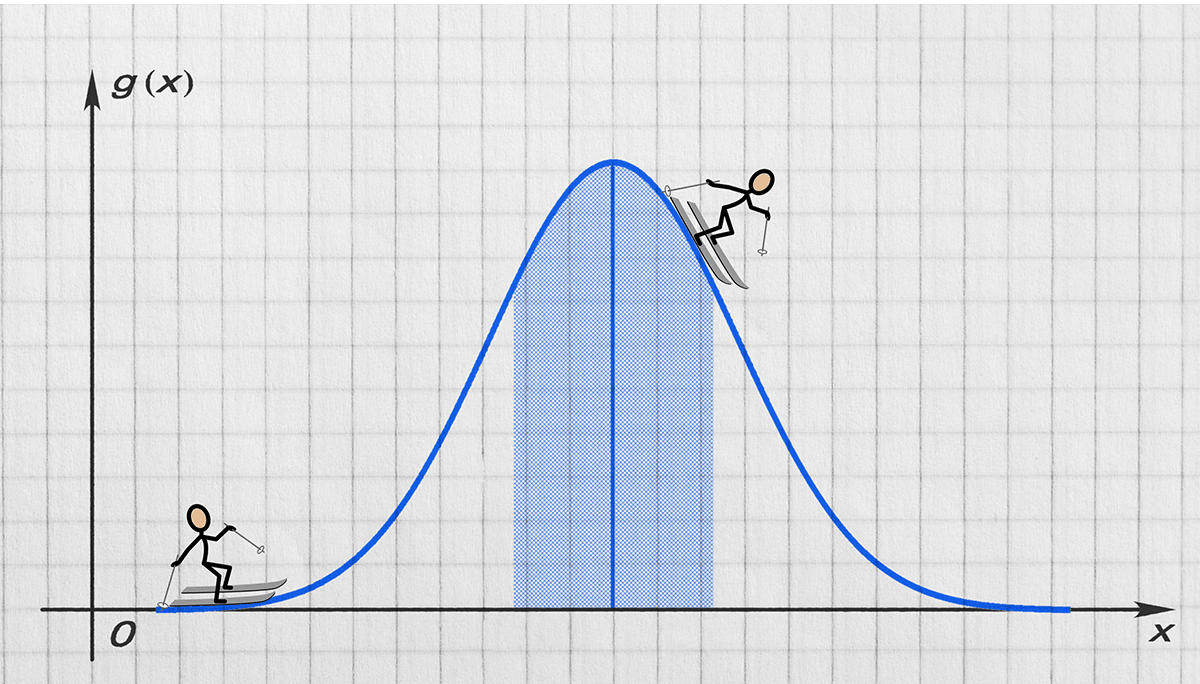
For example, a word problem about finding the slope of a ski hill may include a picture of a person skiing and bundled up with winter clothes. This picture adds helpful context for an ELL student who may not be familiar with skiing or snowy weather. It doesn’t help students understand the mathematics of the problem, but it does serve as an entry point. These kinds of pictures are encouraged when used along with visuals that represent the mathematics of the problem.
A visual representation of the mathematics of this problem may be a sketch of the ski hill with lines drawn to represent the height of the hill and the distance from the base to the finish line. Students would then learn to transfer the diagram to a coordinate plane, identify the x- and y- coordinates, and apply the formulas for determining slope.
Visual Representations and Standards for Mathematical Practice
The Common Core State Standards Initiative has published standards for teaching mathematical content and standards for teaching mathematical practice. Some states follow Common Core and some do not. However, the practice standards are relevant and useful for math teachers across the country. They stand apart from the content standards and describe the broad habits of mathematically proficient students. For example, the first of the eight standards is to make sense of problems and persevere in solving them. The standards are the same from kindergarten through grade 12, and regardless of the math content you teach, you can apply one or more of them.
The use of visual representations can be connected to any of the eight practice standards, but they are strongly emphasized in these three:
- Math.Practice.MP2—Reason abstractly and quantitatively
- Math.Practice.MP4—Model with mathematics
- Math.Practice.MP5—Use appropriate tools strategically
If you use the standards for mathematical practice to shape your philosophy of math instruction and develop strong math habits in your budding mathematicians, this is an important connection to make. Explicitly teaching students how to model and use tools appropriately helps them learn to transfer known skills to novel problems, which can be especially challenging for your unique learners. When students learn to apply visual representations to solve math problems, their math confidence grows. They might even get excited about the challenge of a new problem and learn to love math!



